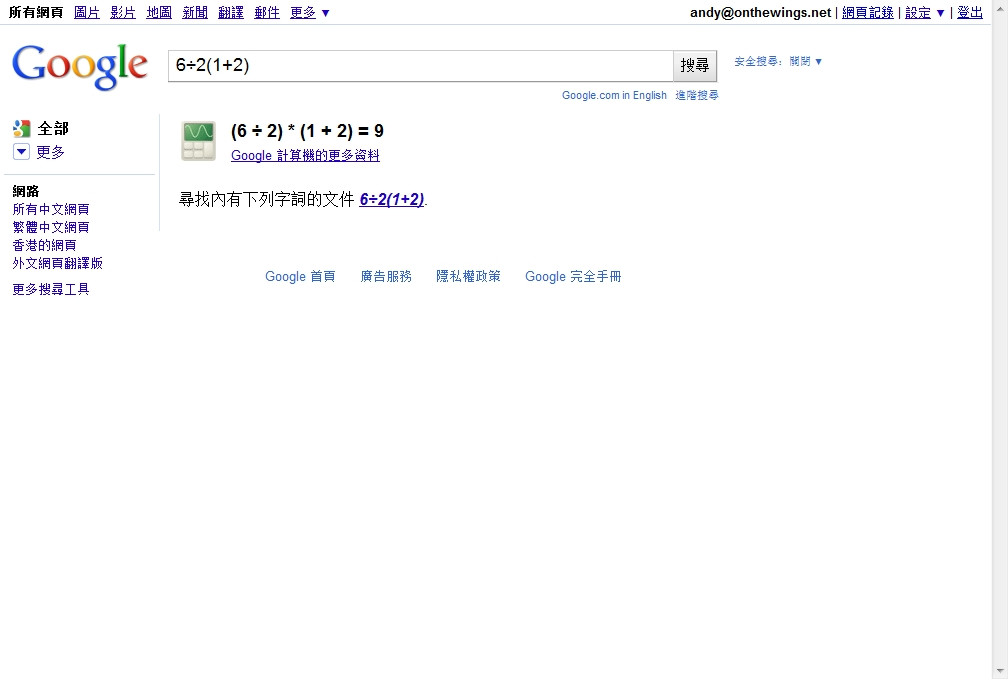
6÷2(1+2)=?
It’s a question that comes around in Facebook recently (I’ve also read it somewhere in the past). There are two major answers: “1” and “9”.
For “1”, (Assuming “multiplication by juxtaposition” has higher precedence than regular division. Whether the assumption is true, is depending on which literature is being referred to. If you don’t agree on it, the answer is simply 9)
6÷(2×(1+2))
=6÷(2×3)
=6÷6
=1
For “9”,
6/2*(1+2)
=6/2*3
=3*3
=9
Notice the question is interpreted differently, you can tell it from looking at the symbols. One is mathematical notation, another is program operator notation.
The difference between mathematics and programming shown above is that, they use different kind of symbols(operators), so they have different order of operation.
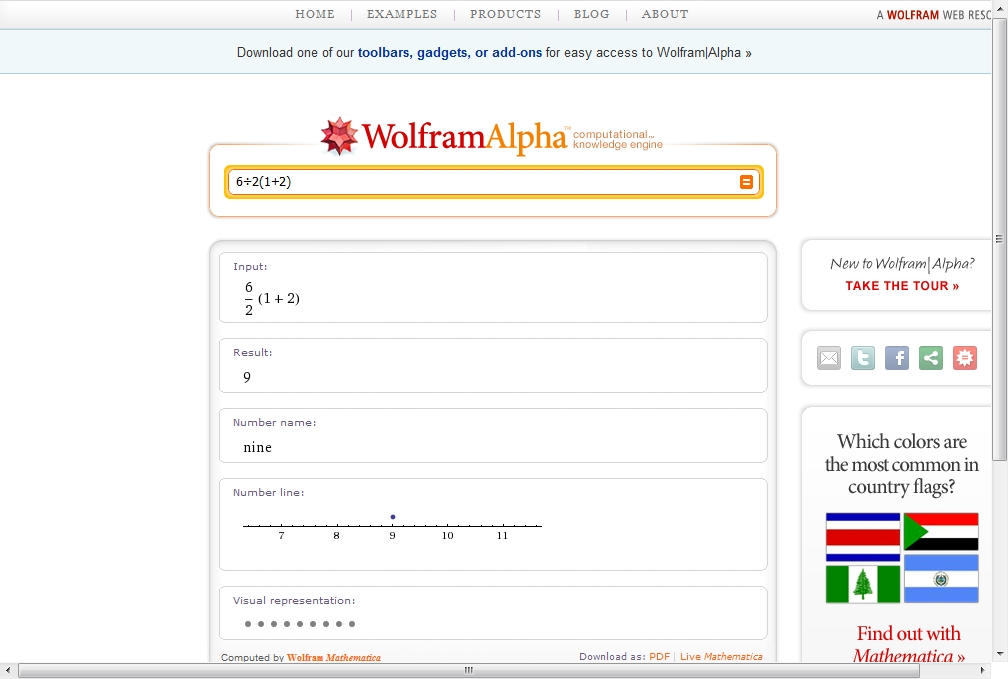
WolframAlpha thinks that is 9:
My Casio calculator thinks that is 1:

One interesting thing is, even in programming, different programming
languages may have different order of operation, i.e. they have different
operator precedence (or operator associativity). The difference is
mostly on bitwise operations(e.g. <<, &, |), and it has been
a nightmare for programmers who want to port algorithms between
languages. And luckily haXe, the language I’m in love with, that
outputs C++/JS/PHP and others, already abstracted the different by
inserting the necessary brackets in the output automatically(see
here). So I’m happily writing codes in haXe and share the same result
in different platforms ;)